Video: Kakšna je vrednost sin 120 v ulomku?
2024 Avtor: Miles Stephen | [email protected]. Nazadnje spremenjeno: 2023-12-15 23:40
Kot vsi vemo, vrednost sinusa nekaterih kotov, kot so: 30, 45, 60, 90, 180. Toda v stopinjah je greh 120 =(✓3)/2. Za to obstaja preprosto pravilo za palec. greh (90+x)=+cos x (od greh x je pozitiven v drugem kvadrantu.)
Podobno, kako najdete vrednost greha 120?
rešitev: greh 120 ° = greh (180° − 120 °) = √3/2. greh 120 °= greh (2×90°-60°)= greh (60°)=√3/2.
In kaj je sin240? 240 stopinj je v tretjem kvadrantu, kjer je greh kota negativen. Če odštejete 180 stopinj od 240 stopinj, lahko vidite, da je referenčni kot 240-180 = 60 stopinj. Greh 60 stopinj je. zato greh 240 stopinj = R^2 pri SCC.
Poleg tega, kakšen je greh 120 stopinj v radianih?
Pomemben povzetek kota
| θ° | θradianov | greh (θ) |
|---|---|---|
| 90° | π/2 | 1 |
| 120° | 2π/3 | √3/2 |
| 135° | 3π/4 | √2/2 |
| 150° | 5π/6 | 1/2 |
Kakšna je natančna vrednost tan 120?
Odgovor in razlaga: The natančna vrednost tan ( 120 °) je -√(3). Od porjavelost ( 120 °) = porjavelost (2 × 60°), lahko uporabimo tangento dvojnega kota za
Priporočena:
Koliko je polovica 3/8 v ulomku?
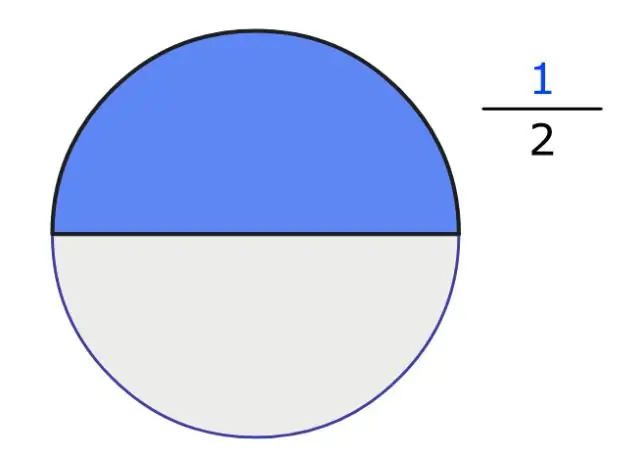
Polovica od 3/8 je preprosto (1/2)×(3/8)
Kakšna je absolutna vrednost minus 3?
Absolutna vrednost 3 je 3. Absolutna vrednost 0 je 0. Absolutna vrednost −156 je 156
Kakšna je natančna vrednost greha 120?
Vrednost Sin120 je √3/2. Kajti lahko ga razdelimo kot sin(90+x), ki leži v drugem kvadrantu, kjer je vrednost sin vedno pozitivna, tako da postane cosx. Torej je odgovor na vprašanje √3/2. Lahko delamo z obema metodama Sin (90+x) in Sin (180-x)
Kaj je polovica 3/4 v ulomku?
"Polovico" ulomka lahko izračunate tako, da podvojite imenovalec (spodnje število * 2), tako da je polovica 3/4 3/8 (formula: polovica a/b je enaka kot a/(b*2), na primer polovica od 3/4 je enaka 3/(4*2), kar je enako 3/8). Druga metoda je, da števec zmanjšate za polovico (zgornje število, deljeno z 2)
Kakšna je natančna vrednost sin 5pi 12?
Odgovor in razlaga: Če želite to narediti, predpostavimo, da je pi r Natančen odgovor je 0,02284431908. Za izpeljavo rešitve moramo najprej rešiti elemente, ki so obdani z oklepaji. Da bi to naredili, predpostavimo, da se pi nanaša na matematično konstanto π π