
- Avtor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:40.
- Nazadnje spremenjeno 2025-06-01 05:06.
Fermatov mali izrek navaja, da če je p praštevilo, potem za katero koli celo število a število a str - a je celo število večkratnik p. astr ≡ a (mod p). Poseben primer: če a ni deljivo s p, Fermatov mali izrek je enakovredna izjavi, da a str-1-1 je celo število večkratnik p.
Kako na ta način dokazati Fermatov mali izrek?
Naj bo p praštevilo in a poljubno celo število, potem astr = a (mod p). Dokaz. Rezultat je trivalen (obe strani sta nič), če p deli a. Če p ne deli a, potem moramo le pomnožiti skladnost v Fermatov mali izrek z a, da dokončate dokaz.
Vedite tudi, kakšna je rešitev Fermatovega zadnjega izreka? Rešitev za Fermatov zadnji izrek . Fermatov zadnji izrek (FLT), (1637), navaja, da če je n celo število večje od 2, potem je nemogoče najti tri naravna števila x, y in z, kjer je taka enakost izpolnjena, če je (x, y)>0 v xn+yn =zn.
Glede na to, zakaj je pomemben Fermatov mali izrek?
Fermatov mali izrek je temeljna izrek v osnovni teoriji števil, ki pomaga izračunati moči celih števil po modulu praštevil. To je poseben primer Eulerjevega izrek , in je pomembno pri aplikacijah osnovne teorije števil, vključno s testiranjem primarnosti in kriptografijo z javnim ključem.
Kaj pomeni Eulerjev izrek?
Eulerjev izrek . Fermatova posplošitev izrek je znan kot Eulerjev izrek . Na splošno, Eulerjev izrek pravi, da "če sta p in q relativno pra, potem ", kjer je φ Eulerjevega Totient funkcija za cela števila. To pomeni, da je število nenegativnih števil, ki so manjša od q in so razmeroma prazna s q.
Priporočena:
Kako v Solidworksu naredite srednjo ravnino?
Funkcije lahko ustvarite s pomočjo srednje ravnine. Pritisnite in držite tipko M in premaknite kazalec. V zbirki znanja SOLIDWORKS poiščite 'Ustvarjanje funkcij s pomočjo srednje ravnine'
Kako naredite raztopino kmno4 za titracijo?
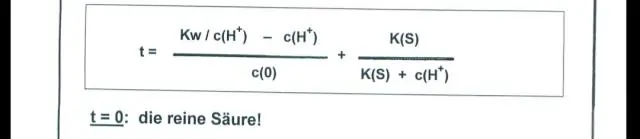
Dodamo 250 ml prečiščene vode (sveže kuhane in ohlajene) in 10 ml žveplove kisline (96 % H2SO4, sp g 1,84). Iz birete hitro dodajte približno 95 % potrebne teoretične količine raztopine kalijevega permanganata; mešajte, dokler raztopina ni bistra
Kako naredite Punnettov kvadrat z več aleli?
Pomembno je, da sledite potrebnim korakom! Najprej morate določiti svoj starševski križ ali P1. Nato morate narediti 16 kvadratnih Punnettov kvadrat za vaši 2 lastnosti, ki ju želite prečkati. Naslednji korak je določiti genotipa obeh staršev in jima dodeliti črke, ki predstavljajo alele
Kako naredite sinusno regresijo na kalkulatorju?
VIDEO Od tega, kako izračunate sinusno regresijo? Sinusoidna regresija . Prilagodite vrednosti A, B, C in D v enačba y = A*sin(B(x-C))+D, da naredimo a sinusni krivulja ustreza danemu nizu naključno generiranih podatkov. Ko imate dobro funkcijo, kliknite »Pokaži izračunano«, da si ogledate izračunano regresija vrstico.
Kako najdete izrek o srednjem segmentu trikotnika?

Izrek o srednjem segmentu trikotnika pravi, da bo odsek, ki povezuje središči poljubnih dveh strani trikotnika, izpolnjeval naslednje lastnosti: Odsek črte bo vzporeden s tretjo stranjo. Dolžina odseka črte bo polovica dolžine tretje strani
